POSTSCRIPT TO EXAMPLES PART III
Bring on the computer!
Otter and Prover9
The background to the invention (c.1965) by J.A.Robinson of his method of proof by unification and resolution was his interest in computer-assisted reasoning. The method was incarnated in a computer program designed by Robinson and others working at the Argonne National Laboratory in Illinois, USA. An eventual successor was the late W.McCune's program OTTER (standing for Organized Techniques for Theorem-proving and Effective Research) which evolved in turn into Prover9, which is freely available on the internet.
Now, our investigation of Example 10.10 involved quite a few complex unifications, which became quite tiresome to work through by hand. It may well have occurred to the reader that it would be much preferable to hand over this work to a machine. Fortunately Prover9, even if it is designed to achieve far higher things, remains capable of calculating simple proofs by resolution - essentially using the 'breeding' process described in Chapter 4 (Resolution in CLS).
I was curious about a rather specific question: what would happen to our proof by resolution of the statement ∀x Rxex if our rather specific premise Rxixhx were to be replaced by the more general P0 stating that for all x and y there exists a z such that x•y = z? I started to work through this by hand; but at a certain point I decided that this was a problem for a computer (not me), and downloaded Prover9. (To be specific, the version I downloaded was the latest version that is provided with a Graphical User Interface, dating from December 2007 and described on this page.) I suggest that you do the same.
When you've done so, get acclimatized by trying out some of the sample theorems included in the program. To do this, click on File/Sample/Non-equality and choose an example. The 'Assumptions' (=premises) and 'Goals' (=conclusion) appear on the 'Formulas' tab. To start the search for a proof, click on the 'Start' button near the right-hand side of the window. If the search is successful, the proof comes up in a new window. The text of the proof has been processed by a bolt-on program called ProofTrans, and there are some options such as renumbering the clauses and expanding the proof into simple binary resolutions.
To try out your own assumptions and goals, type them into the indicated areas on the Formulas tab, using the conventions exemplified by the sample theorems.
These are the assumptions and goals which I typed in:
%Assumptions R(x,y,c(x,y)) # label(P0). R(e,x,x) # label(P3). R(i(x),x,e) # label(P4). -R(x,y,u)|-R(y,z,v)|-R(u,z,w)|R(x,v,w) # label(P1). -R(x,y,u)|-R(y,z,v)|-R(x,v,w)|R(u,z,w) # label(P2). -R(u,v,w1)|-R(u,v,w2)|-R(w1,x,y)|R(w2,x,y) # label(E12). %Goals R(x,e,x) # label(right_id).
A few observations are in order. The Prover9 convention is that lower-case letters taken from the far end of the alphabet (u onwards) represent variables, while letters from the near end represent constants. If you run out of letters for variables use strings that start with a suitable letter (i.e. u onwards). Instead of subscripts (as in CLS) use the familiar function-with-arguments notation in which the arguments are enclosed in paretheses and separated by commas. A minus sign - is used for 'not', & for 'and', | for 'or'. The way that P1, for example, is represented, as "not-Rxyu or not-Ryzv or not-Ruzw or Rxvw", will be seen to be not that dissimilar to the way it is represented in CLS, i.e.
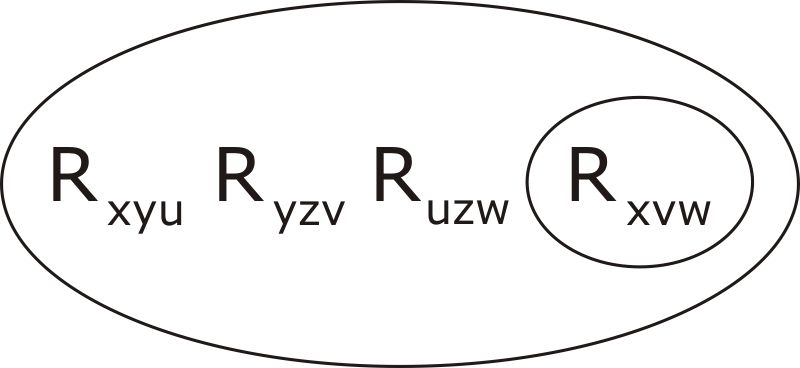
In P0, the function c(x,y) corresponds to the subscripted constant cxy; in P3, e corresponds to e. The single premise E12 replaces the separate premises E1 and E2 (the idea was to make things easier for Prover9). It says: "if uv is w1, and uv is w2, and w1x is y, than w2x is also equal to y".
Then I pressed 'Start'. Quick as anything a proof came back:
============================== prooftrans ============================ Prover9 (32) version Dec-2007, Dec 2007. Process 4148 was started by GnJ on GnJ-PC, Mon Mar 2 12:17:40 2015 The command was "/cygdrive/c/Program Files (x86)/Prover9-Mace4/bin-win32/prover9". ============================== end of head =========================== ============================== end of input ========================== ============================== PROOF ================================= % -------- Comments from original proof -------- % Proof 1 at 0.01 (+ 0.01) seconds: right_id. % Length of proof is 9. % Level of proof is 3. % Maximum clause weight is 16. % Given clauses 8. 1 R(x,e,x) # label(right_id) # label(non_clause) # label(goal). [goal]. 3 R(e,x,x) # label(P3). [assumption]. 4 R(i(x),x,e) # label(P4). [assumption]. 5 -R(x,y,z) | -R(y,u,w) | -R(z,u,v5) | R(x,w,v5) # label(P1). [assumption]. 6 -R(x,y,z) | -R(y,u,w) | -R(x,w,v5) | R(z,u,v5) # label(P2). [assumption]. 8 -R(c1,e,c1) # label(right_id) # answer(right_id). [deny(1)]. 9 R(i(i(x)),e,x). [ur(5,a,4,a,b,4,a,c,3,a)]. 53 R(x,e,x). [ur(6,a,9,a,b,3,a,c,9,a)]. 54 $F # answer(right_id). [resolve(53,a,8,a)]. ============================== end of proof ==========================
The extraordinary thing is that P0 and E12 are not used at all! Moreover, the program has found an extremely short route to our goal. The only really meaty steps are the ones that lead to the clauses labelled 9 and 53. It is basically a two-line proof.
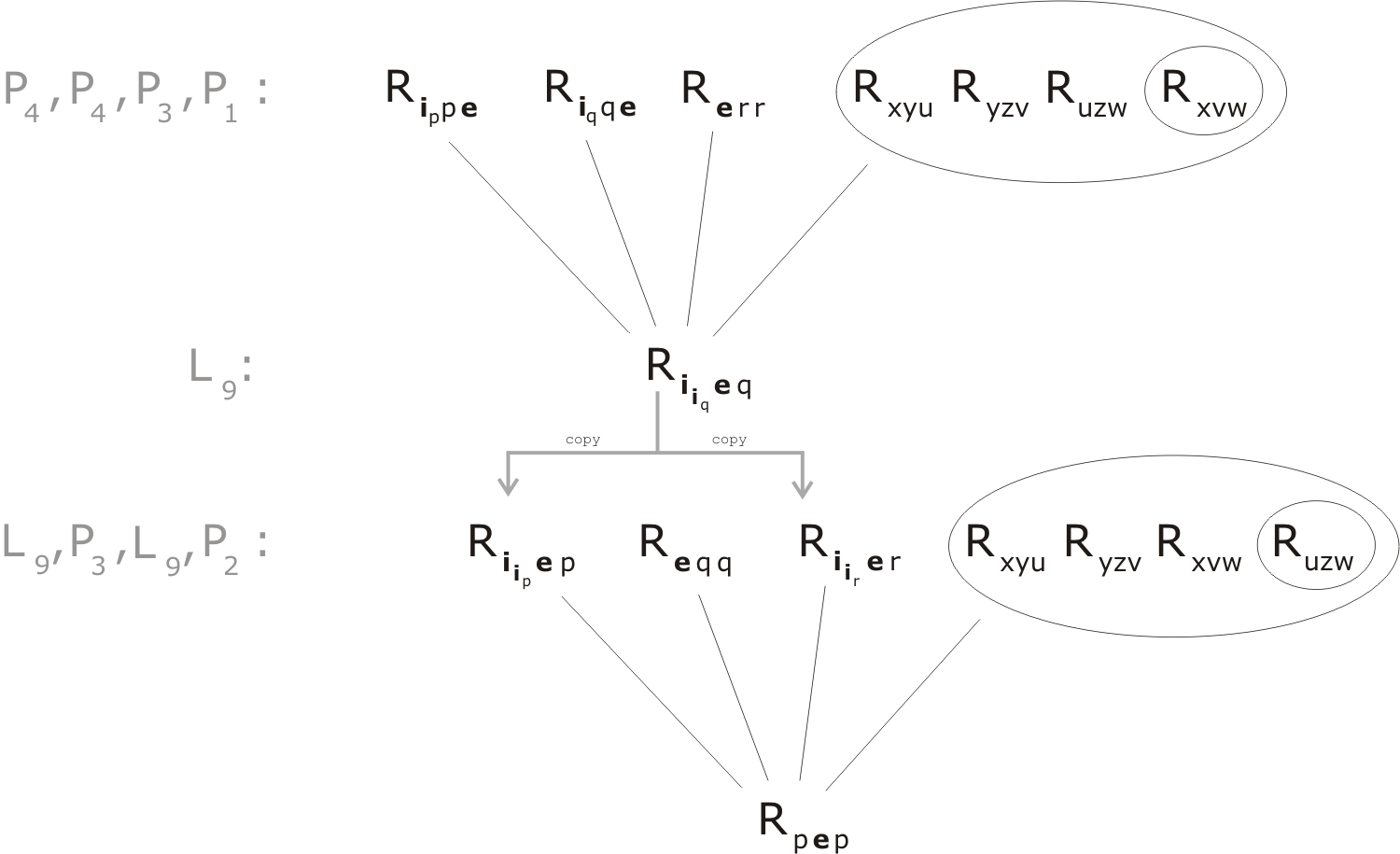
Let's do some decoding of the reasoning leading to these clauses. 'ur' stands for 'unit-resolution' which evidently means (on this occasion, at least) something very similar to what we have called 'compound resolution'. In case of clause 9, the clauses employed as premises are numbers 5, 4, 4 and 3. Clause 5 is the premise P1, 4 and 3 are P4 and P3. So let's see what happens if we do a compound resolution of these premises:
Res(P4, P4, P3, P1);
a question of unifying
Rxyu Ryzv Ruzw with Rippe Riqqe Rerr .
This requires the substitutions:
x = ip y = p = iq ∴ x = iiq z = q = r u = e v = e w = r = q
leading to
Rxvw = Riiqeq .
The conclusion agrees with clause 9; let us denote it L9.
We go on to consider the derivation of clause 53, from clauses 6, 9, 3 and 9. We're looking at
Res(L9, P3, L9, P2),
requiring us to unify
Rxyu Ryzv Rxvw with Riipep Reqq Riirer ,
determining the following substitutions:
x = iip = iir ∴ r = p y = e z = q u = p v = q = e ∴ z = e w = r = p
Therefore,
Ruzw = Rpep .
The proof is so short we can represent it in a single diagram:
Translating it into a 'natural language' proof, and representing the element (x-1)-1
by the
abbreviation x+1 we have:
L9: x+1e = x+1(x-1x) =
(x+1x-1)x = ex = x
[by P4, associativity, P4, P3]
C: xe = (x+1e)e = x+1(ee) = x+1e = x
[by L9, associativity, P3, L9]
A two-line proof indeed!◊
Exercise for the reader
Take as given the four group axioms (left-unit, left-inverse, assoc1, assoc2), and define equality as follows:
Exy ↔ ∃u ∃v Ruvx ∧ Ruvy.
Prove in turn the following three properties of the equality relation:
(i) Exy ∧ Rxuv → Ryuv
(ii) Exy ∧ Ruxv → Ruyv
(iii) Exy ∧ Ruvx → Ruvy.
Hint: if you get into difficulties, resort to Prover9. (For those without access to Prover9, its output is given here. If you manage to come up with natural language proofs, I will be interested to hear from you via the contact page.)